Liste de spirales mathématiques

Cette liste de spirales mathématiques inventorie les noms, les images et quelques propriétés de spirales définies en mathématiques et dessinées en dimension deux ou trois.

Spirales du plan

Image	Nom	Équation	Année	Commentaires
	Cercle	Équation polaire : $\rho =R$		Spirale triviale
	Spirale d'Archimède	Équation polaire : $\rho =a+b\cdot \theta ,\theta >0$	Vers -300	Étudiée par Archimède puis PappusModèle:Sfn. Courbe ayant une origine, pas de fin et des spires régulièrement espacées
	Spirale de Fermat	Équation polaire : ${\rho }^2=a^2\theta ,\theta >0$	1636Modèle:Sfn	Étudiée par Pierre de FermatModèle:Sfn. Deux branches infinies symétriques.
	Spirale hyperbolique	Équation polaire : $\rho =\frac{a}{\theta },\theta \ne 0$	1704Modèle:Sfn	Étudiée par Pierre VarignonModèle:Sfn. Deux branches infinies symétriques. Un point et une droite asymptotes.
	Lituus	Équation polaire : ${\rho }^2\theta =a^2,\theta >0$	1722Modèle:Sfn	Étudiée par Roger CotesModèle:Sfn. Dessinée ci-contre pour Modèle:Mvar positif. Le point O et la droite (Ox) sont asymptotes.
	Spirale de Galilée	Équation polaire : $\rho =a-b{\theta }^2$	1636Modèle:Sfn	Étudiée par Fermat pour un problème posé par GaliléeModèle:Sfn.
	Spirale logarithmique	Équation polaire : $a{\mathrm{e}}^{b\theta }$	1638Modèle:Sfn	Première mention chez René Descartes, puis étudiée par Marin Mersenne,John Wallis et Jacques Bernoulli. Une branche infinie, un point asymptote. Appelée spirale équiangle et spira mirabilis pour ces nombreuses propriétés géométriques.
	Spirale d'or	Équation polaire : $\rho =a{\phi }^{\frac{2}{\pi }\theta }$ où Modèle:Mvar est le nombre d'or		Cas particulier de spirale logarithmique.
	Développante du cercle	Équations paramétrées: $\{\begin{array}{c}x(t)=r(\cos t+t\sin t)\\ y(t)=r(\sin t-t\cos t).\end{array}$	1693Modèle:Sfn	Étudiée par Christian HuygensModèle:Sfn.
	Clothoïde	Équations paramétréesModèle:Sfn: $\{\begin{array}{c}x(t)=\underset{0}{\overset{t}{\int }}\sin \left(\frac{u^2}{2a^2}\right)\mathrm{d}u\\ y(t)=\underset{0}{\overset{t}{\int }}\cos \left(\frac{u^2}{2a^2}\right)\mathrm{d}u.\end{array}$	1694	Étudiée par Jacques Bernoulli, puis par Leonhard Euler, Augustin Fresnel, Alfred Cornu et Ernesto Cesàro. Porte également le nom de Spirale d'Euler, Spirale de Fresnel et Spirale de Cornu. Deux points asymptotes.
	Spirale de Poinsot de type borné	Équation polaire: $\rho =\frac{C}{\cosh (k\theta )}$	1834Modèle:Sfn	Étudiée par Louis Poinsot Courbe bornée possédant un point asymptote. Cas particulier de spirale de Cotes
	Spirale de Poinsot de type asymptote	Équation polaire: $\rho =\frac{C}{\sinh (k\theta )}$	1834	Étudiée par Louis Poinsot Courbe possédant un point et une droite asymptotes. Cas particulier de spirale de Cotes., appelée par Teixeira Spirale de la cosécante hyperboliqueModèle:Sfn.
	Spirale tractrice	Équation polaire: $\theta =\pm (\frac{\sqrt{a^2-{\rho }^2}}{\rho }-\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}\frac{\rho }{a})$ avec $0<|\rho |<a$ .	1707	Étudiée par Varignon et par CotesModèle:Sfn, baptisée par Teixeira. Courbe dont la tangente polaire est de longueur constante Modèle:Mvar. C'est aussi une tractoire dont la base est un cercle de rayon Modèle:Mvar/2 et de distance Modèle:Mvar/2.
	Spirale de Pritch-Atzema	Équations paramétrées: $\{\begin{array}{c}x(t)=\frac{R}{2}(\frac{\sin t}{t}-2\cos t-t\sin t)\\ y(t)=\frac{R}{2}(-\frac{\cos t}{t}-2\sin t+t\cos t).\end{array}$ où Modèle:Mvar est le rayon du cercle catacaustique	2011	Courbe dont la caustique en flambeau par réflexion est un cercle: le rayon issu du point noir et se réfléchissant sur la courbe est tangent au cercle rouge.
	Escargot de Pythagore		vers -400	Appelée aussi Spirale de Théodorus qui l'a étudiée. Construit géométriquement les racines carrées de tous les entiers.
	Spirale à centres multiples			Succession d'arcs de cercles jointifs dont les centres sont sur les sommets d'un polygone régulier. Construction préconisée pour le dessin de volutes
	Spirale de Fibonacci			Succcession de quarts de cercle jointifs dont les rayons sont des éléments de la suite de Fibonacci. Bonne approximation d'une spirale d'or.
image	nom	équation	date	commentaires

Spirales et hélices de l'espace

Remarque : dans toute la suite, les équations données en coordonnées sphériques utilisent les notations suivantes

• Modèle:Mvar pour la distance au pôle;
• Modèle:Mvar pour la colatitude;
• Modèle:Mvar pour la longitude.

Image	Nom	Équation	Année	Commentaires
	Hélice circulaire	Équations paramétrées: $\{\begin{array}{cc}x(t)& =a\cos (t)\\ y(t)& =aϵ\sin (t)\\ z(t)& =bt\end{array}$	vers 300	Étudiée par Pappus d'Alexandrie et AppoloniusModèle:Sfn. Les tangentes font un angle constant avec les directrices.
	Hélice conique	Équations sphériques: $\{\begin{array}{c}\rho =a{\mathrm{e}}^{b\phi }\\ \theta =\alpha \end{array}.$ où Modèle:Mvar est le demi-angle au sommet du cône.	1845	Étudiée par Olry Terquem. Appelée aussi loxodromie coniqueModèle:Sfn ou hélice cylindro-coniqueModèle:Sfn. Sa projection sur le plan de base est une spirale logarithmique. Ses tangentes font un angle constant avec l'axe du cône.
	Spirale de Pappus conique	Équations sphériques: $\{\begin{array}{c}\rho =a\phi \\ \theta =\alpha \end{array}.$ où Modèle:Mvar est le demi-angle au sommet du cône.	vers 300	Étudiée par Pappus, Blaise Pascal et Michel Chasles. Teixeira l'appelle aussi «hélice conique»Modèle:Sfn. Sa projection sur le plan de base est une spirale d'Archimède.
	Spirale de Pappus sphérique	Équations sphériquesModèle:Sfn: $\{\begin{array}{c}\theta =\frac{\phi }{4}\\ \rho =R\end{array}.$	vers 300	Étudiée par Pappus. Cas particulier de clélie avec pour paramètre Modèle:Formule.
	Clélie (spirale)	Équations sphériquesModèle:Sfn: $\{\begin{array}{c}\theta =m\phi \\ \rho =R\end{array}.$	1728Modèle:Sfn	Étudiée par Luigi Guido Grandi. Parfois appelée spirale (d'Archimède) sphérique. Sa projection sur le plan de base est une rosace.
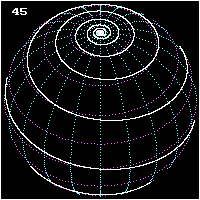	Loxodromie de la sphère	Équations paramétrées: $\{\begin{array}{cc}x(t)& =R\frac{\cos t}{\mathrm{c}\mathrm{h}kt}\\ y(t)& =R\frac{\sin t}{\mathrm{c}\mathrm{h}kt}\\ z(t)& =R\mathrm{t}\mathrm{h}kt\end{array}$ où ch et th sont respectivement les fonctions cosinus hyperbolique et tangente hyperbolique et où $k=\mathrm{c}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{n}\alpha$	1537	Courbe étudiée par Pedro Nunes, Simon Stévin et Maupertuis qui fait un angle constant Modèle:Mvar avec les méridiens. Sa projection sur l'équateur est une spirale de Poinsot bornée
image	nom	équation	date	commentaires

Bibliographie

• Modèle:Ouvrage

  traduit de l’original en espagnol de 1899, revu et très augmenté. Réédition: dans les Obras sobre Matemática, volume V, 1908–1915; Chelsea Publishing Co, New York, 1971; Éditions Jacques Gabay, Paris, 1995 Modèle:Lire en ligne.

• Modèle:Mathcurve